Bài 4.16 trang 74 Toán 7 tập 1
Cho hai tam giác ABC và DEF thoả mãn (AB = DE,AC = DF,widehat {BAC} = widehat {EDF} = {60^circ },BC = 6;{rm{cm}},widehat {ABC} = {45^circ }). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Hướng dẫn giải:
Xét hai tam giác ABC và DEF có:
(begin{array}{l}AB = DEAC = DFwidehat {BAC} = widehat {EDF} = {60^circ }end{array})
(Rightarrow Delta ABC = Delta DEF(c.g.c))
Do đó:
EF = BC = 6cm
(widehat {DEF} = widehat {ABC} = {45^o})
(begin{array}{l}widehat {BAC} + widehat {ABC} + widehat {ACB} = {180^o} Rightarrow {60^o} + {45^o} + widehat {ACB} = {180^o} Rightarrow widehat {ACB} = {75^o}end{array})
(Rightarrow widehat {EFD} = widehat {ACB} = {75^o})
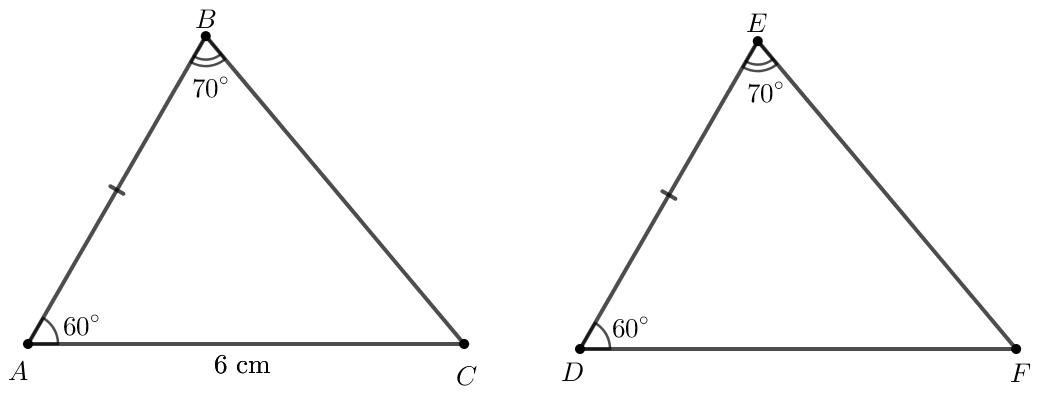
Bài 4.17 trang 74 Toán 7 tập 1
Cho hai tam giác ABC và DEF thoả mãn (AB = DE, widehat {ABC} = widehat {DEF} = {70^circ },widehat {BAC} = widehat {EDF} = {60^circ },AC = 6;{rm{cm}}).
Tính độ dài cạnh DF.
Hướng dẫn giải:
Xét hai tam giác ABC và DEF có:
(begin{array}{l}widehat {ABC} = widehat {DEF} (= {70^circ })AB = DEwidehat {BAC} = widehat {EDF} (= {60^circ })end{array})
(Rightarrow Delta ABC{rm{ = }}Delta DEF(g.c.g))
(Rightarrow DF = AC) (2 cạnh tương ứng)
Mà AC = 6 cm
(Rightarrow DF = 6cm)
Bài 4.18 trang 74 Toán 7 tập 1
Cho Hình 4.44, biết EC = ED và (widehat {AEC} = widehat {AED}). Chứng minh rằng:
(begin{array}{*{20}{l}}{{rm{ a) }}Delta AEC = Delta AED;}&{{rm{ b) }}Delta ABC = Delta ABD.}end{array})
Hướng dẫn giải:
a) Xét hai tam giác AEC và AED có
EC = ED
(widehat {CEA} = widehat {DEA})
AE chung
(Rightarrow Delta AEC{rm{ = }}Delta AED(c.g.c))
b) Do (Delta AEC{rm{ = }}Delta AED) nên (widehat {CAE} = widehat {DAE}) (2 góc tương ứng) và AC=AD (2 cạnh tương ứng).
Xét (Delta ABC) và (Delta ABD) có:
AB chung
(widehat {CAE} = widehat {DAE})
AC=AD
(Rightarrow Delta ABC = Delta ABD(c.g.c))
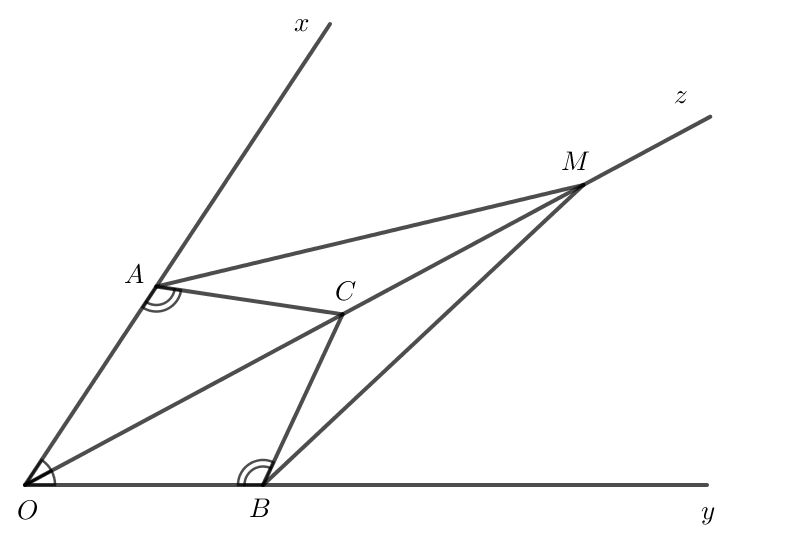
Bài 4.19 trang 74 Toán 7 tập 1
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho (widehat {CAO} = widehat {CBO}).
a) Chứng minh rằng (Delta OAC = Delta OBC).
b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng (Delta MAC = Delta MBC).
Hướng dẫn giải:
a) Xét (Delta OAC) và (Delta OBC) có:
(widehat {AOC} = widehat {AOB})(Oz là phân giác góc xOy)
OC chung
(widehat {CAO} = widehat {CBO})
(Rightarrow Delta OAC = Delta OBC(g.c.g))
b) Do (Delta OAC = Delta OBC) nên AC=BC (2 cạnh tương ứng)
Vì (widehat {ACO}) và (widehat {ACM}) kề bù
(widehat {BCO}) và (widehat {BCM}) kề bù
Mà (widehat {ACO} = widehat {BCO}) nên (widehat {ACM} = widehat {BCM})
Xét (Delta MAC) và (Delta MBC) có:
AC=BC
(widehat {ACM} = widehat {BCM})
CM chung
(Rightarrow Delta MAC = Delta MBC(c.g.c))
.............................
Chuyên mục Giải bài tập Toán 7 trên VnDoc tổng hợp lý thuyết và lời giải cho các bài tập trong SGK Toán 7 giúp các em nâng cao kỹ năng giải Toán lớp 7. Mời các em tham khảo để học tốt môn Toán lớp 7 hơn nhé. Ngoài ra, các bạn có thể tham khảo thêm các Tài liệu học tập lớp 7 và các đề thi học kì 1, đề thi học kì 2 lớp 7 được cập nhật liên tục trên VnDoc.
