Tổng hợp kiến thức cơ bản về hình thang và hình thang cân

Hình thang là một hình tuy đơn giản nhưng lại có nhiều tính chất phức tạp vì nó bao gồm nhiều trường hợp đặc biệt và định lý cần ghi nhớ. Vậy nên phần lý thuyết và bài tập của hình thang đều tương đối khó và đòi hỏi chúng ta phải nắm chắc kiến thức về đường thẳng song song, tam giác bằng nhau, đường trung bình, trung tuyến… Hôm nay, Gia Sư Việt sẽ tổng hợp các kiến thức cơ bản về hình thang và hình thang cân giúp các em hiểu rõ từng khái niệm, tính chất và cách chứng minh nhé.

I. Hình thang

1. Khái niệm về hình thang

Hình thang là tứ giác có hai cạnh đối song song.

Từ hình vẽ, ta thấy: Hình thang cân ABCD có AB // CD

2. Tính chất hình thang

- Tính chất 1: Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ (nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là 2 cạnh đáy).

Ví dụ: Hình thang ABCD (AB // CD)

=> Góc A + Góc D = Góc B + Góc C = 180°

- Tính chất 2: Hình thang có 2 cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.

Ví dụ: Hình thang ABCD (AB // CD) có AB = CD

Xét tứ giác ABCD có: AB // CD và AB = CD

=> ABCD là hình bình hành nên AD // BC và AD = BC

Ngược lại, nếu hình thang có 2 cạnh bên song song thì chúng sẽ bằng nhau và 2 cạnh đáy bằng nhau.

Ví dụ: Hình thang ABCD (AB // CD), lại có AD // BC

Xét tứ giác ABCD có: AB // CD và AD // BC

=> ABCD là hình bình hành nên AB = CD và AD = BC

- Tính chất 3: Đường trung bình là đường thẳng nối trung điểm hai cạnh bên của hình thang.

Ví dụ: Hình thang ABCD (AB // CD) có E là trung điểm AD, F là trung điểm BC

=> MN là đường trung bình của hình thang ABCD

Tính chất 3.1: Đường thẳng đi qua trung điểm 1 cạnh bên của hình thang và song song với 2 cạnh đáy thì sẽ đi qua trung điểm của cạnh bên còn lại.

Ví dụ: Hình thang ABCD (AB // CD) có E là trung điểm AD, EF //AB (EF // CD) (F ∈ BC)

=> F là trung điểm BC

Tính chất 3.2: Đường trung bình của hình thang sẽ song song với 2 cạnh đáy và bằng 1/2 tổng 2 đáy.

Ví dụ: Hình thang ABCD (AB // CD) có EF là đường trung bình

=> EF// AB; EF // CD và EF = (AB+CD)/2

3. Cách chứng minh hình thang

- Cách 1: Chứng minh tứ giác đó có một cặp cạnh đối song song.

Ví dụ: Cho hình thang ABCD (AB // CD). Gọi E là giao điểm của hai đường thẳng AD và BC. Gọi M, N, P, Q theo thứ tự là các trung điểm của các đoạn thẳng AE, BE, AC và BD. Chứng minh tứ giác MNPQ là hình thang.

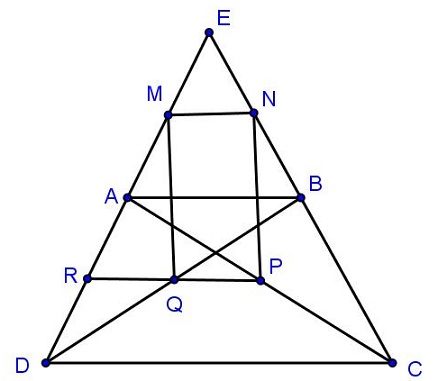
Ta có:

M là trung điểm của AE

N là trung điểm của BE

=> MN là đường trung bình ứng với cạnh AB của ΔEAB, suy ra MN // AB (1)

Gọi R là trung điểm của AD

Trong ΔADB, RQ là đường trung bình, suy ra RQ // AB

Trong ΔCAD, RP là đường trung bình, suy ra RP // DC

mà DC // AB nên RP // AB.

RQ và RP cùng đi qua R và cùng song song với AB nên theo tiên đề Ơclit thì RQ ≡ RP

Từ đây ta suy ra QP // AB (2)

Từ (1) và (2) suy ra MN // PQ => Tứ giác MNPQ là hình thang do một cặp cạnh đối song song.

- Cách 2: Chứng minh tứ giác đó có tổng hai góc kề một cạnh bên bằng 180 độ.

Ví dụ: Cho tam giác ABC. Trên AC lấy một điểm B’ sao cho AB’ = AB và trên AB lấy một điểm C’ sao cho AC’ = AC. Chứng minh tứ giác BB’CC’ là hình thang.

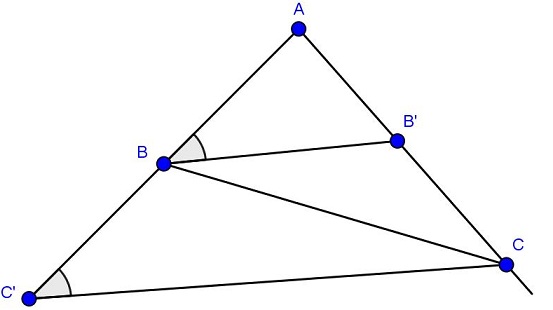
Ta có:

AB’ = AB

=> ∆BAB’ cân tại A

=> Góc ABB’ = (180°- Â)/2

Chứng minh tương tự, ta có: Góc AC’C = (180°- Â)/2

=> Góc ABB = Góc AC’C

=> Góc ABB’ + Góc B’BC’ = Góc AC’C + Góc B’BC’

=> Góc AC’C + Góc B’BC’ = 180°

=> Tứ giác BB’CC’ là hình thang do tổng hai góc kề một cạnh bên bằng 180°

II. Hình thang cân

1. Khái niệm về hình thang cân

Trong hình học Euclid, hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau. Hình thang cân là 1 trường hợp đặc biệt của hình thang.

Từ khai niệm và theo hình vẽ, ta có:

Hình thang cân ABCD (AB // CD) => Góc C = Góc D

2. Tính chất hình thang cân

- Tính chất 1: Trong một hình thang cân, hai cạnh bên bằng nhau.

Ví dụ: ABCD là hình thang cân (AB // CD)

=> AD = BC

- Tính chất 2: Trong một hình thang cân, hai đường chéo bằng nhau.

Ví dụ: Cho ABCD là hình thang cân (AB // CD)

=> AC = BD

- Tính chất 3: Hình thang cân luôn nội tiếp được trong một đường tròn.

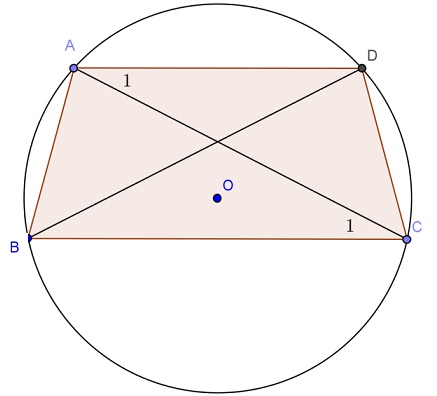
Ví dụ: ABCD là hình thang cân (AB // CD)

=> Luôn có một đường tròn tâm O nội tiếp hình thang này

3. Cách chứng minh hình thang cân

- Cách 1: Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.

Ví dụ: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE. Chứng minh rằng BDEC là hình thang cân.

a) Ta có: AD = AE (gt) nên ∆ADE cân

⇒ Góc D2 = Góc E2

Mà góc A + D2 + E2 = góc A + B + C = 180°, trong khi góc B = C do ΔABC cân tại A (gt). Vì vậy D2 = B ( vị trí đồng vị )

=> DE // BC, do đó BDEC là hình thang.

Lại có ΔABC cân tại A ⇒ Góc B = Góc C

Nên BDEC là hình thang cân là là hình thang có 2 góc đáy bằng nhau.

- Cách 2: Hình thang có hai cạnh bên bằng nhau là hình thang cân.

Ví dụ: Hình thang ABCD (AB // CD) nội tiếp đường tròn tâm O. Chứng minh rằng ABCD là hình thang cân.

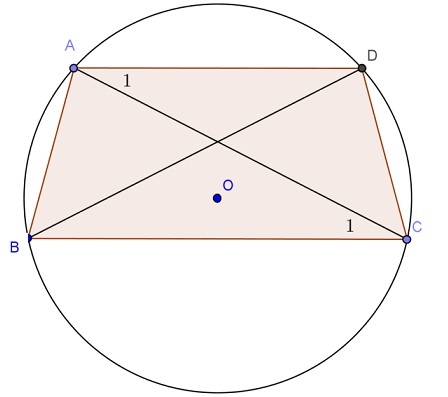
Ta có: ABCD là hình thang

=> Góc A1 = Góc C1

=> sđ cung CD = sđ cung AB

=> AB = CD

=> ABCD là hình thang cân do là hình thang có 2 cạnh bên bằng nhau.

- Cách 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ: Hình thang ABCD (AB // CD) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân.

Gọi E là giao điểm của AC và BD.

∆ECD có góc ACD = góc BDC nên là tam giác cân.

Suy ra EC = ED (1)

Tương tự xét ∆EAB có: Góc ABE = BAE do cùng đều bằng góc ACD và góc BDC ( So le trong )

⇒ ∆EAB tại E suy ra: EA = EB (2)

Từ (1) và (2) ta có: EA + EC = EB + ED => AC = BD

=> ABCD là hình thang cân do là hình thang có 2 đường chéo bằng nhau

Kết luận: Sau khi các em học sinh đã được tìm hiểu các kiến thức cơ bản về hình thang và hình thang cân. Chúng tôi tin rằng, nội dung này sẽ không làm khó các bạn nữa và giúp đạt được điểm số tối đa trong mỗi bài thi. Hãy theo dõi Gia Sư Việt để học luôn cập nhập nhiều bài học khác nhé. Ngoài ra, nếu phụ huynh cần thuê gia sư dạy Toán tại nhà cho con, vui lòng liên hệ qua số 096.446.0088 - 090.462.8800 để được tư vấn chi tiết.

Tham khảo thêm:

♦ Tổng hợp kiến thức về các đường Đồng quy trong Tam giác

♦ Khái niệm, tính chất và cách chứng minh tứ giác là Hình thoi